Abstract
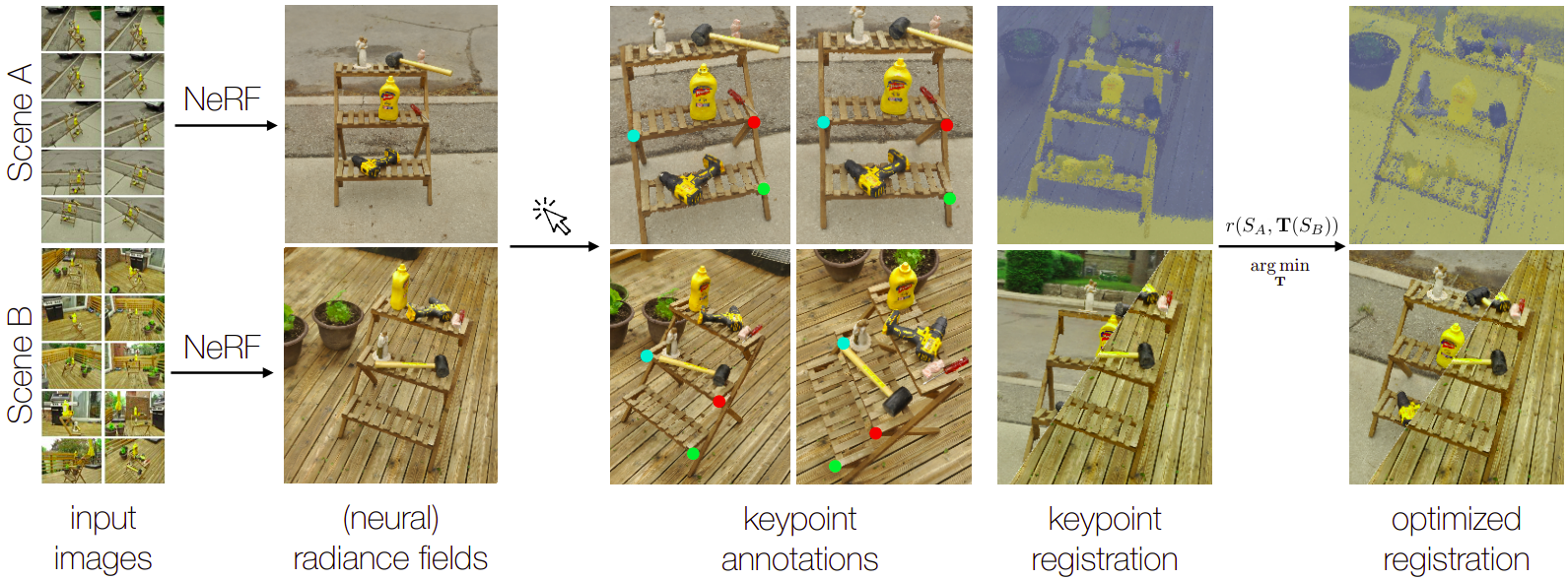
We introduce a technique for pairwise registration of neural fields that extends classical optimization-based local registration (i.e. ICP) to operate on Neural Radiance Fields (NeRF) – neural 3D scene representations trained from collections ofcalibrated images. NeRF does not decompose illumination and color, so to make registration invariant to illumination, we introduce the concept of a “surface field” – a field distilled from a pre-trained NeRF model that measures the likelihood of a point being on the surface of an object. We then cast nerf2nerf registration as a robust optimization that iteratively seeks a rigid transformation that aligns the surface fields of the two scenes. We evaluate the effectiveness of our technique by introducing a dataset of pre-trained NeRF scenes – our synthetic scenes enable quantitative evaluations and comparisons to classical registration techniques, while our real scenes demonstrate the validity of our technique in real-world scenarios.
Surface Field
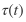 of a point t measures the differential probability of hitting a particle
of a point t measures the differential probability of hitting a particle 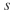 at a point (view-independent). Transmittance
at a point (view-independent). Transmittance 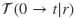 is the probability that a ray
is the probability that a ray 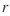 hits no solid particle on its way to the point (view-dependent), and can be derived directly from density through integration along the ray. Using the multiplication theorem for independent events, we can then define the differential probability of hitting a surface while looking from a certain viewing direction as the product of density and transmittance (view-dependent):
hits no solid particle on its way to the point (view-dependent), and can be derived directly from density through integration along the ray. Using the multiplication theorem for independent events, we can then define the differential probability of hitting a surface while looking from a certain viewing direction as the product of density and transmittance (view-dependent):
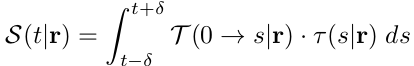
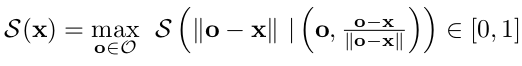
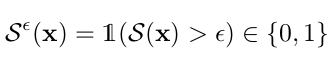
Energy-based Optimization
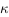 and apply it on our residuals.
and apply it on our residuals.
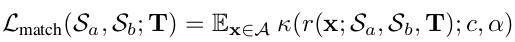
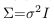 , and derive
, and derive 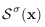 . The residual is then efined using this smooth surface field:
. The residual is then efined using this smooth surface field:
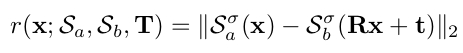
Sampling
Results
| Bench | Bust | Jar |
Video
Citation
Acknowledgements
The website template was borrowed from Dor Verbin.
